(UPDATE 10/11/11 -For French translation of this post please click "here.")
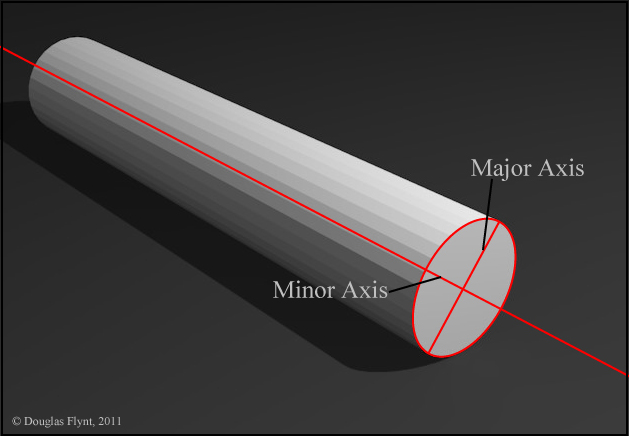
For this post I wanted to expand on my previous post that addressed drawing ellipses—an element so critical to my own paintings. In the previous post I illustrated the “major” and “minor” axes of an ellipse, showed that an ellipse or circle in perspective could be constructed at the picture plane, and offered a geometrical construct to aid us in drawing ellipses regardless if they are 2-dimensional (at the picture plane) or in perspective. If the reader is unfamiliar with those items reading the previous post might prove useful before going further. Here is a link to the previous post:
For this post I wanted to expand on my previous post that addressed drawing ellipses—an element so critical to my own paintings. In the previous post I illustrated the “major” and “minor” axes of an ellipse, showed that an ellipse or circle in perspective could be constructed at the picture plane, and offered a geometrical construct to aid us in drawing ellipses regardless if they are 2-dimensional (at the picture plane) or in perspective. If the reader is unfamiliar with those items reading the previous post might prove useful before going further. Here is a link to the previous post:
After drawing or painting a great number of still-life elements it becomes evident that the placement and orientation of the major and minor axes are critical to constructing an accurate ellipse within a drawing or painting. In my own work I largely free hand the drawing rather than setting up a careful perspective framework and then make use of my perspective knowledge to inform and correct the decisions I make.
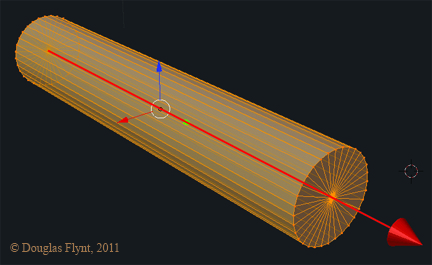
Before going further I should clarify that the following discussion addresses circular, cylindrically shaped objects (cylinders with cross sections that form perfect circles) rather than forms derived from elliptical cylinders, also know as “cylindroids,” whose cross sections are elliptical. It should also hold true for right angle cones that have circular cross sections.
Once we know this center axis spatially we need to visualize the angle or line that we would perceive at the picture plane for this axis. This will also be the visual line of symmetry for the outside contour or silhouette of the object.
Working 2-dimensionally at the picture plane, this line will run through the minor axis of any ellipses we might need to draw for that object. We then know that the major axis will run perpendicular to the line we found. Now that we know the orientation of both axes, once we visually determine their lengths we can construct a perfect ellipse for any of the circles that we see in perspective!
This all might seem rather self evident for a glass of water sitting upright directly in front of you but as you encounter cylindrically based objects that are spatially rotated to more unconventional positions guessing the orientation of the major and minor axes can at times become rather tricky and I have found that this simple understanding and assessment greatly aids me in my own work. Here are some cylinders (and a cone) to illustrate a few more examples:
Thanks for taking a look!





Great informative post, Douglas. Thank you as always for your generous information sharing!
ReplyDeleteMay I also point out, as I think it may be of some use to artists, that when you view an ellipse the further half is slightly smaller than the nearer half. This is important to know for naturalistic ellipses. The difference is slight, but if this isn't taken into account when drawing it makes the ellipse appear odd, or even distorted.
ReplyDelete