Accurate Ellipses

(UPDATE 10/11/11 -For French translation of this post please click "here.") 

I finished up teaching a still life workshop at the Grand Central Academy of Art about a week ago.  While there one of the items we discussed were drawing accurate ellipses in our still-lifes.  I thought I would share some of that information here.  This information has been of great use to me while drawing cylindrically based objects such as cups and jars in my own still-lifes 

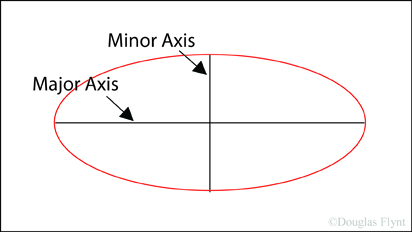
One of the first things we need to know is some terminology pertaining to ellipses.  The widest distance across an ellipse is known as the "major axis" while the shortest distance is known as the "minor axis."  For a circle the major axis and the minor axis would be the same distance.

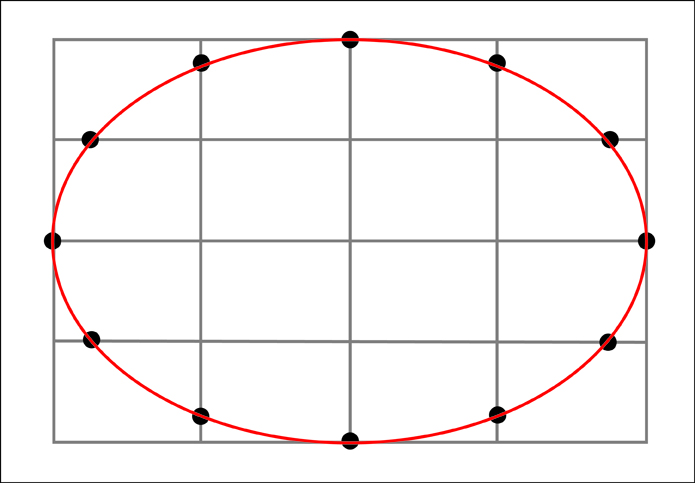
With this shared terminology, it is interesting to note that if we take an ellipse and place it in perspective the resulting curvature we perceive is no different than if we were to construct an ellipse at the "picture plane" using the dimensions of the major and minor axes as they appear at this picture plane.  The image below shows a circle in perspective on the left and the resulting ellipse that we would see at the picture plane on the right. The curvature of both are the same. 

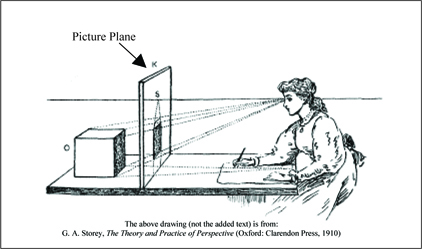
As a quick side note, for those of you unfamiliar with the term picture plane, in perspective it is the imaginary flat surface that is located between the viewer and the object being viewed.  The drawing below from G.A. Storey's 1910 book, The Theory and Practice of Perspective gives a good visualization for imagining a picture plane.

Returning to our ellipses, because the ellipse found in perspective and the ellipse constructed at the picture plane both create the same curvature we don't actually have to construct the circles or ellipses we see within our still-lifes in perspective—it should however be noted that the ability to do so is a valuable aid to our conceptual comprehension.  Instead, and here is the important part, to draw a ellipse or circle being viewed in perspective we only need to know the dimensions of the major and minor axes as they are perceived at the picture plane.  With these dimensions we can correctly construct an ellipse at the picture plane which will correspond to the ellipse or circle being viewed in perspective.

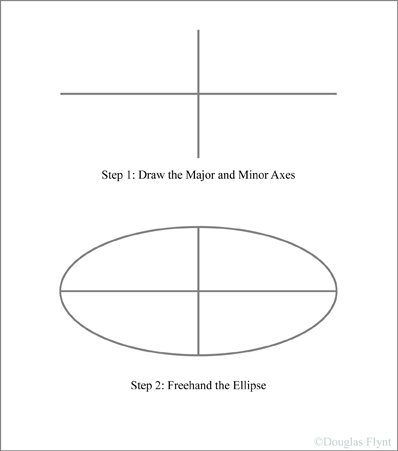
With this knowledge in tow, for now let us only work at the picture plane and construct an ellipse.  There are many ways to construct ellipses yet there are two main ways that I usually find myself constructing them (or very often correcting freehanded versions of them).  If they are rather small I often just draw the major and minor axes in and then carefully freehand the ellipse checking the symmetry of both sides as I go.    

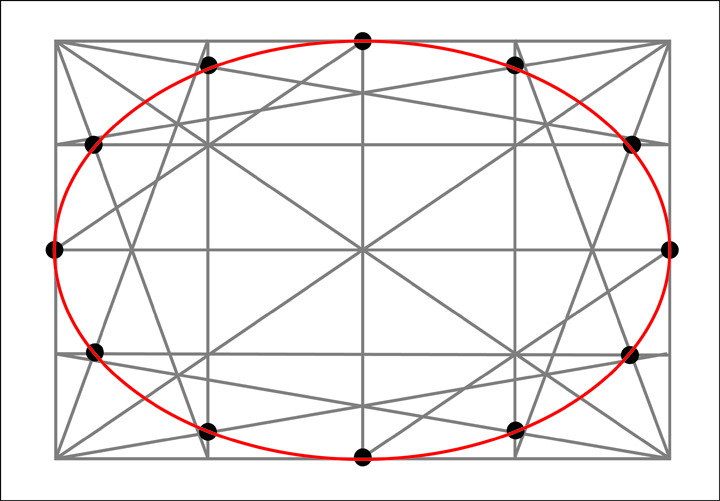
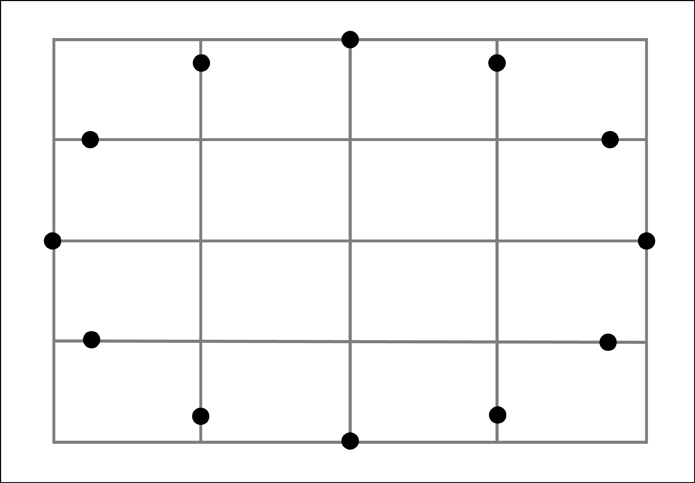
For larger ellipses I construct the following geometrical frame work which gives me 12 points along the ellipse to guide any freehanded approximations.  

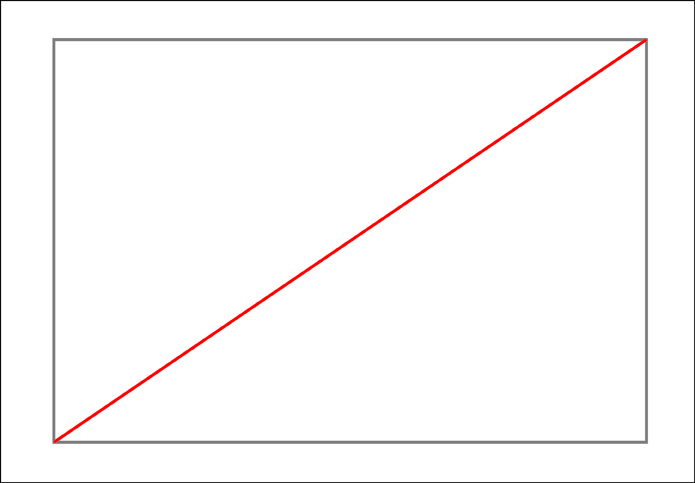
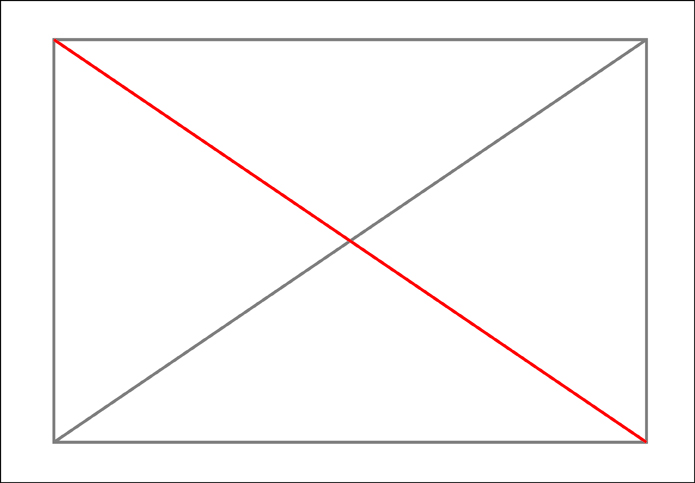
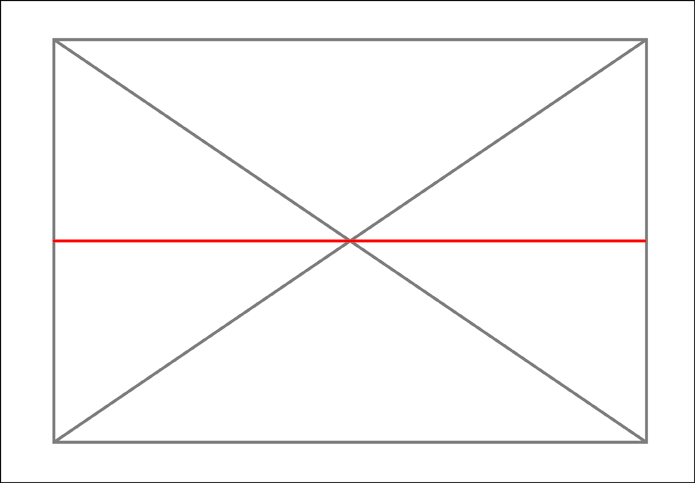
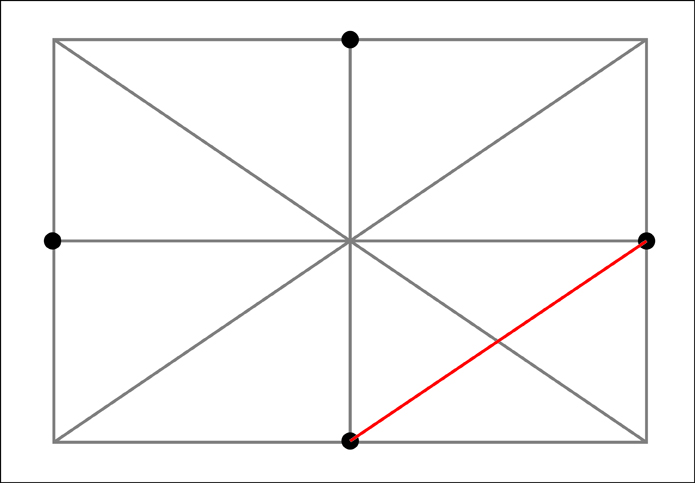
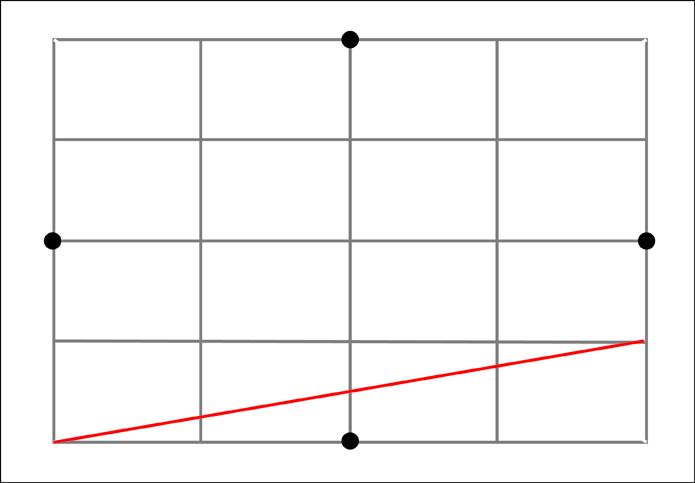
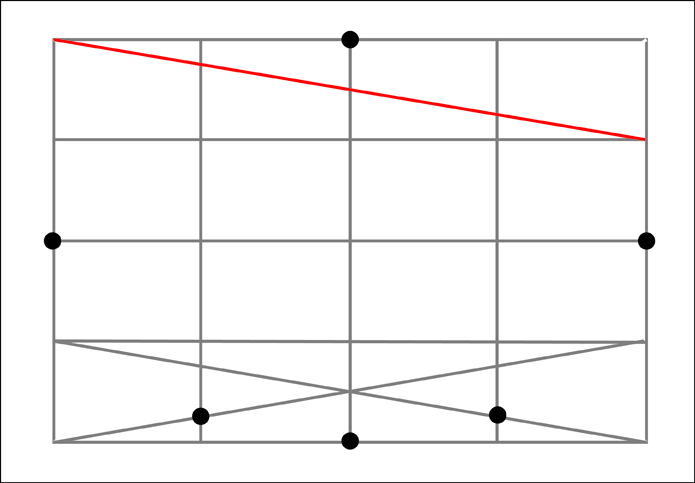
To make the framework I need to first create a rectangle with the proportions of the major and minor axes of the ellipse.  I then need to divide this rectangle into 16 equal sections.  To make these sections it is useful to remember that a simple “X” created from diagonal corners of the rectangle will always find the center of that rectangle.  Along the way we will also gain 4 of our 12 points that make up the ellipse.

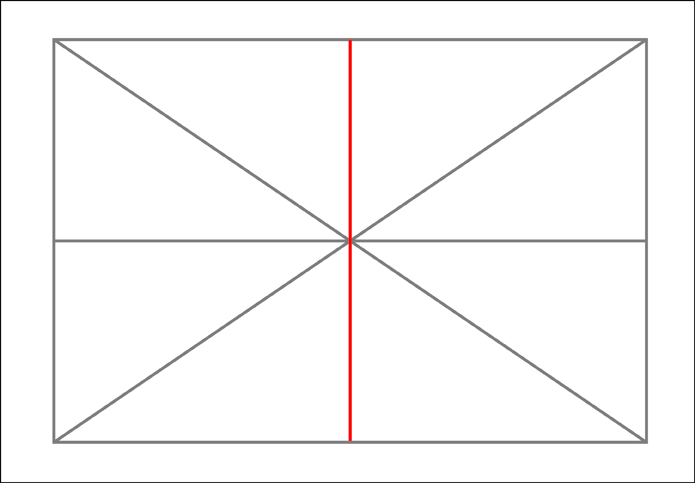
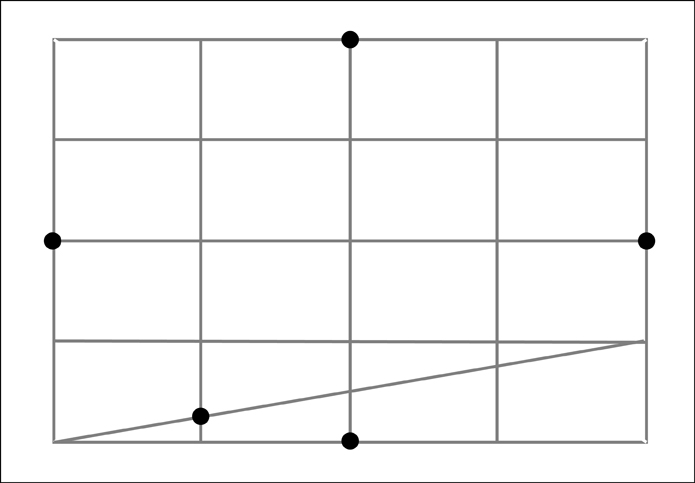
At this point we now know 4 of our points and we have divided our rectangle into 4 equal sections.  We now need to divide each of those sections into four more sections.

We now have 16 equal sections.  However, before going further let's remove the diagonals used in constructing those sections to keep things from getting too visually confusing.

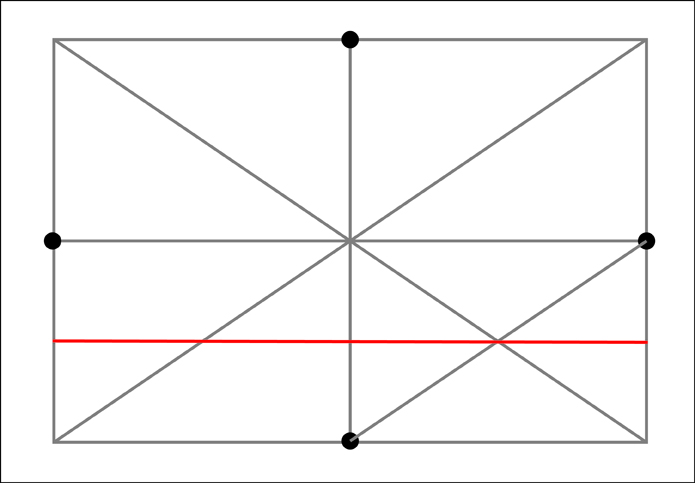
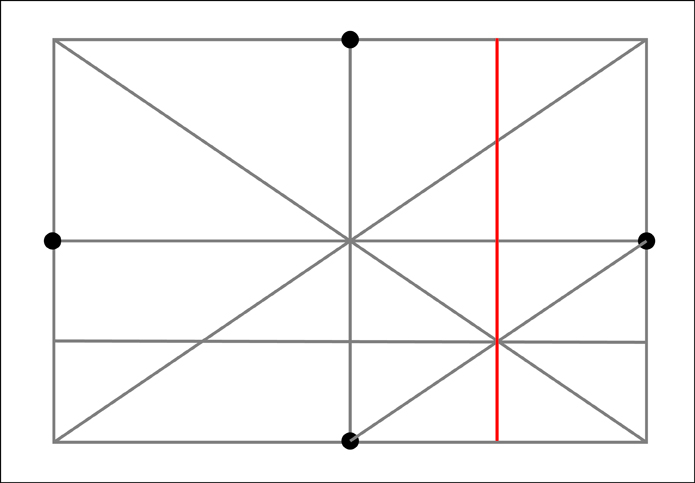
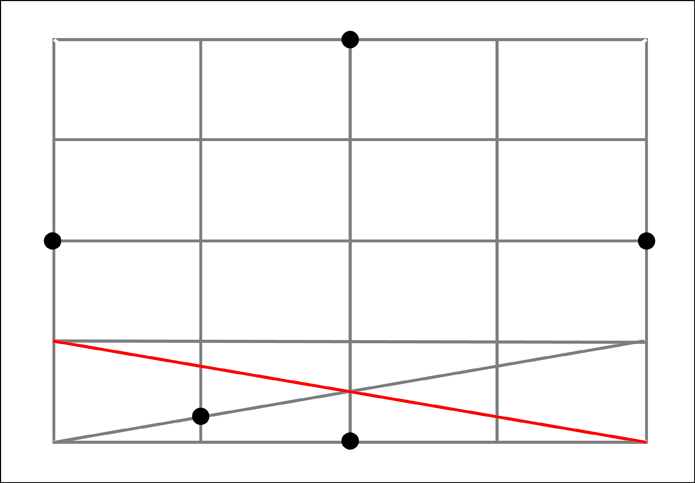
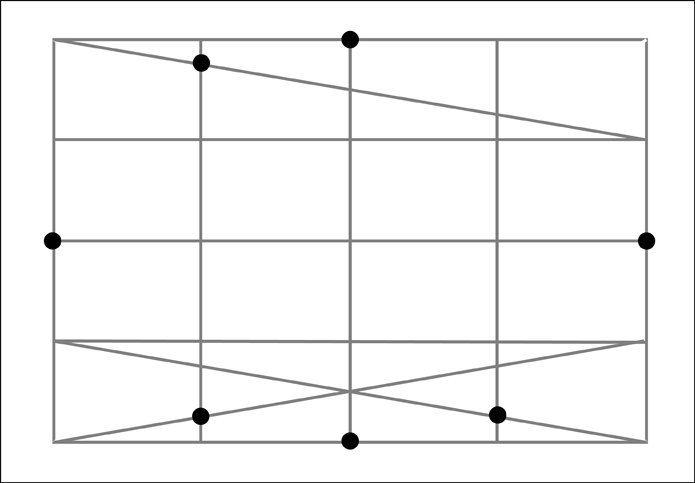
To find the remaining 8 additional points we need to run diagonal lines across the 4 outer sections along each side. Next note where these diagonals intersect the boundaries between the outer four sections of that particular side.  At these intersections, the one that is the closest to the outside of our original rectangle will also mark a point along our ellipse.  Let's start with the bottom section.

Now for the top section.

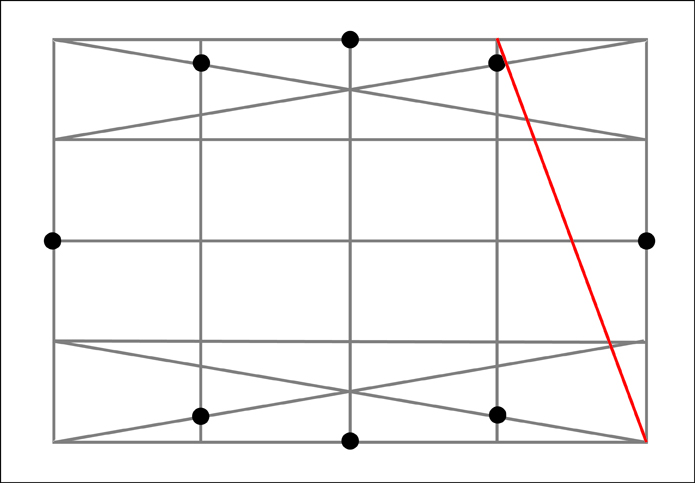
The right section.

And finally the left section.

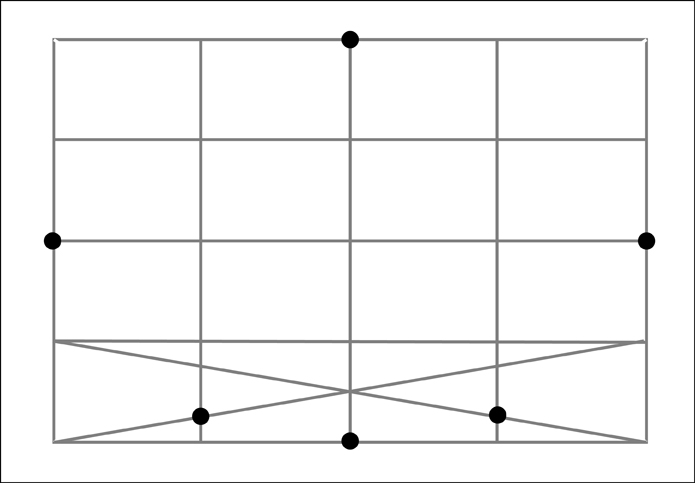
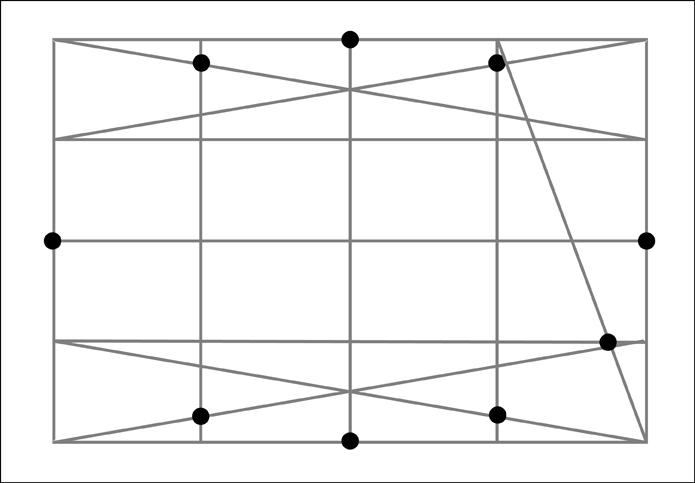
Once again, for clarity let's remove the diagonals used to find the additional points.

And finally we now have 12 points we can use to aid us in drawing our ellipse!

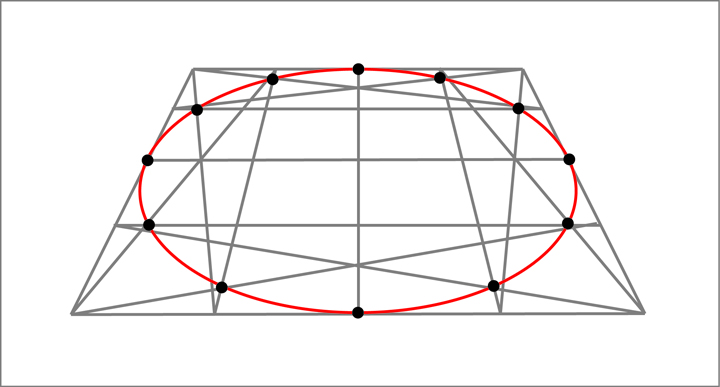
Leaving the picture plane behind, it is useful to know that this same process works just as well to draw ellipses or circles that are in perspective.

This knowledge has been a resource which I have found very useful in my drawings and paintings.  After a couple of times rehearsing the process it becomes fairly easy to commit to memory.  Additionally, after constructing a number of ellipses in this formal and structured way I suspect that most people will begin to get more accurate results when free-handing them without such a complex framework. 

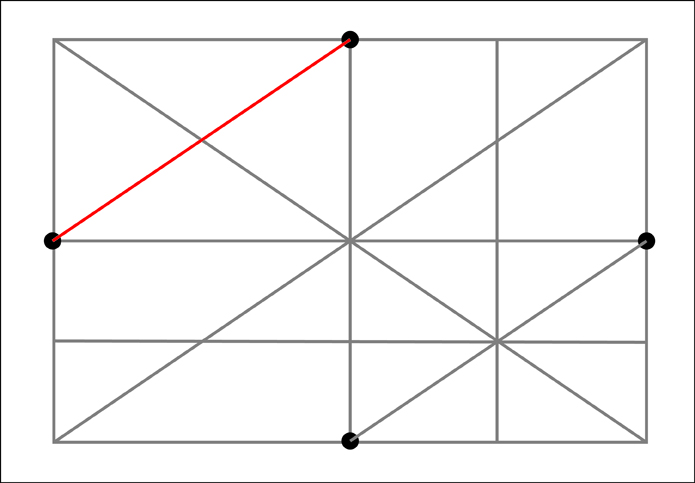
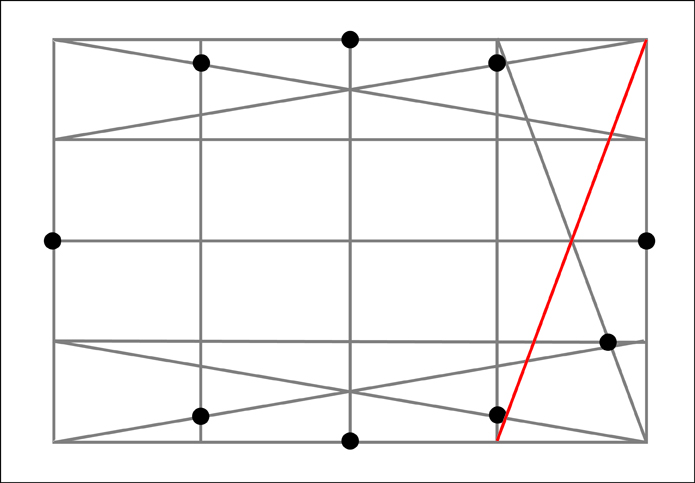
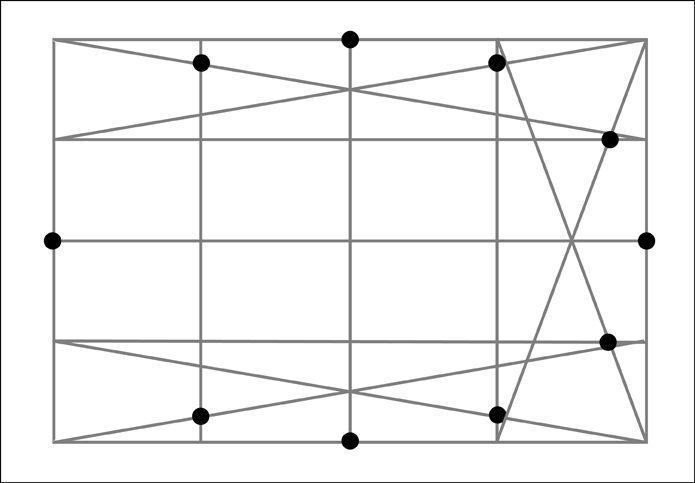
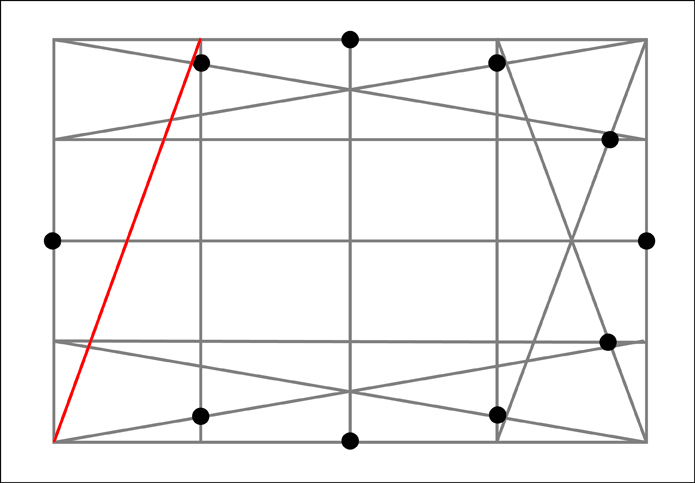
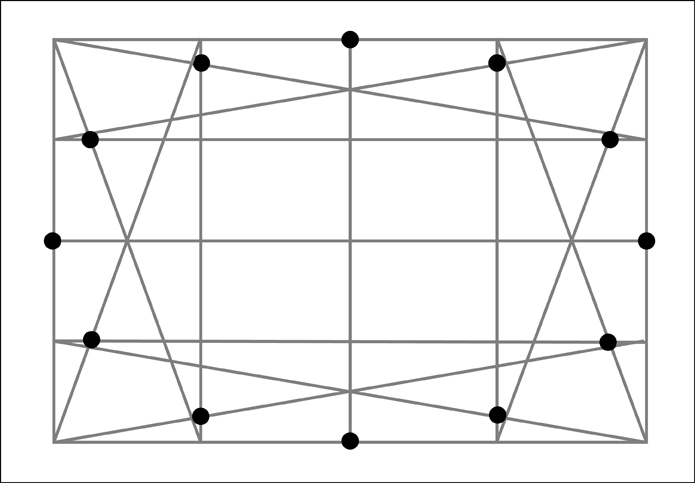
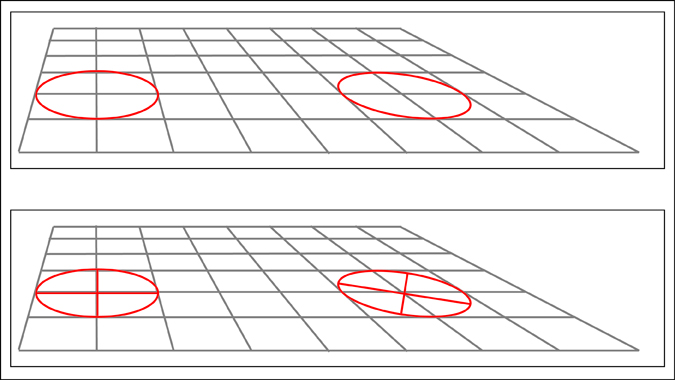
Going even further, some of you may have already picked up on the fact that the ellipses I have shown in perspective have thus far been in one point perspective with an ellipse that would be directly in front of us (the viewer).   It is interesting to note what happens when the ellipse is moved left or right from this center position. In doing so the major and minor axes of the ellipse (as seen at the picture plane) will begin to rotate.  They do however continue to stay perpendicular to one another.   

There is still plenty more to share on this subject however my busy schedule means that I will have to return to the subject at another time.  Yet I hope some of you will benefit from what I have been able to share.  And as always, thanks for visiting.

Did you enjoy this post?

Join My E-mail List