The Composition of Light and J. G. Vibert

(UPDATE 10/27/11 -For French translation of this post please click "here.")
I was recently reading "The Science of Painting" by J. G. Vibert and came across a section where he discusses understanding the local color of an object in terms of the color spectrum of light and which wavelengths are absorbed vs. reflected. Here is a brief excerpt:

"If, on the contrary, a body sends back a part of the light received, and decomposes the rest, the colour of the coloured ray or of the mixture of coloured rays which it will send back will be of a colour more or less light, according to the quantity of light sent back.

Example: —A body which sends back the half of the light received, decomposing the remainder, and sending back only the red ray, gives the impression of half-white and a seventh of half-red, i.e. pink."

J. G. Vibert, The Science of Painting, trans. (from 8th edition) and ed. J. G. Vibert (London: Percy Young, 1892), 22

Online text of book:
http://books.google.com/books?id=LO8DAAAAYAAJ&printsec=frontcover&dq=The+science+of+painting+vibert&source=bl&ots=VGmKXHT7wr&sig=D__AAeHVIyvRXcOwfiA4uYgFh14&hl=en&ei=IjdMTIGxOoS8lQeNwMj4DQ&sa=X&oi=book_result&ct=result&resnum=1&ved=0CBcQ6AEwAA#v=onepage&q&f=false

Images of J. G. Vibert's work:
http://www.artrenewal.org/pages/artist.php?artistid=134
I found the text interesting because I sometimes think of a model which examines the light wavelengths present to keep track of the appearance of an object's color (in terms of hue, value and chroma). I make use of this model both in my own work and also in my teaching and thought I might share some of that information here.

I should point out that this model is not entirely truthful when dealing with the resulting color we perceive based upon the composition of light. I will endeavor to clarify this problem later in the post. Despite this flaw, as a model, it consistently works to keep track of how the color of an object appears to change based on the light it receives and then reflects.

As I have discussed in previous posts, light is composed of many different wavelengths and for our model I am going to classify them into 6 groups, namely red, orange, yellow, green, blue, and violet

(Note: This is different from Vibert who uses 7 colors—perhaps influenced by the writings of Newton.)

Newton's Color Wheel

To visualize the model I think of the colors in the form of a bar graph. All of the bars together add up to 100%. However, each bar individually only contributes about 16.7%. If all colors of light are present in a very high degree this translates to appearing very light in value. In this same scenario because all wavelengths are present they will neutralize one another giving the appearance of a neutral (achromatic) color. In this situation the resulting color would appear white.

(Note: The percentages of light in the diagrams and the resulting color are highly approximated. They are mainly for offering a rough visualization of the concept being discussed)

The absence of light would of course appear as black.

With less overall light present but all colors in equal proportion the result would still be chromatically neutral but darker in value—giving the appearance of a grey.

Along these lines and speaking in terms of the appearance of objects as composed from their reflected light, rather than the light source itself, Vibert offers the following:

"A body which absorbs part of the light and sends back the rest is grey. The whitest objects, therefore, are only very light grey, and the blackest very dark grey. However, the light which a grey body sends back is the same as that which is sent back by a white body: the difference is merely in quantity."

J. G. Vibert, The Science of Painting, trans. (from 8th edition) and ed. J. G. Vibert (London: Percy Young, 1892), 21

Continuing with the model being presented, if only one color is present the result will be that hue. Because there are no other colors present this color will be at its highest chromatic intensity. However since there is less light present overall it will have darkened in value.

As there is less light of this particular color present it will continue to darken in value and appear to weaken in chroma.

If one color is present in it's full percentage but we add back in the other colors in equal proportion this increase in the amount of light will cause the value to lighten but the chroma to weaken.

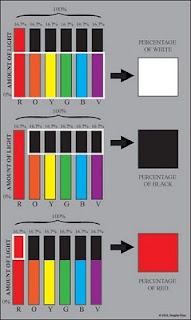
In looking at the model it may be useful to imagine the percentage of all colors equally present as equaling that percentage of white, the absence of light as equaling that percentage of black, and the percentage of color(s) present individually (not already included with our white percentage) as equaling the percentage of that color. By then combining these together we get some sense of what the resulting color might be. The following diagram should make this easier to grasp.

It needs to be mentioned that this model of light as it has been presented so far is based on the composition, or mixture, of wavelengths an object would reflect assuming full illumination. With less illumination, such as is found upon planes of an object "turning" from a light source, this "mixture" would be the same, but there would be less of the "mixture" overall. The result would cause the appearance of the local color's mixture to darken in value and weaken in chroma.

I mentioned earlier that there is an untruth with this model. This untruth lies in the fact that our perceptions of colors are due to combinations of various wavelengths so that just because we see a color does not mean that those light waves are actually present. A great example is that the screen you are viewing is composed of only 3 colors of light which are red, green and blue. Despite this you have experienced the color of orange in the diagrams I offered. However for our purposes the model will yield consistent perceptual results in trying to understand the relative changes to the appearance of objects when observing the loss or addition of certain assumed wavelengths—for instance when dealing with reflected light since the reflected light will have a different composition of wavelengths than the original light source.

There are many ways we can use this model to help explain what we see but they are more than I can post at this time. Perhaps in a future post I can use the model to explain particular examples—for instance how the reflected light from an object reflecting back onto itself can cause the object to appear even higher in chroma, even when there is less light present such as in a shadow.

Thanks for taking a look.